08.11.09
Some max/no mark examples
After the last post, several people mentioned that they were confused about how the “max/no mark” upper bound on the highest score in a class of Boggle boards worked. With some help from OmniGraffle, I’ve created some instructive examples.
Here’s a class of boards:
| f | {a,u} | r |
| . | . | e |
| . | . | . |
The dots mean “no letters here”. The class contains two different boards:
|
|
It contains two boards. The one with an “a” has two points worth of words on it, while the one with a “u” only has one. (We’re only looking at words starting with ‘f’ here.)
The diagrams show that the solver starts with the ‘f’ on each board and explores adjacent cells. When it finds a word, it scores it and passes the total score back up the depth-first search tree.
Here’s how the max/no mark bound sees that board class:
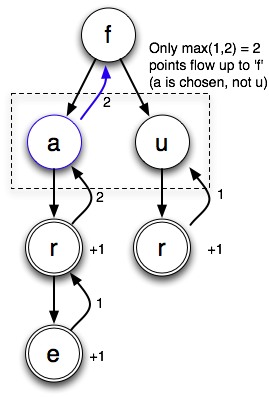
When it gets to the “{a,u}” cell, it tries both possible letters. The “a” tree brings back 2 points, whereas the “u” tree brings back 1 point. So it chooses “a” and counts two points. As it so happens, this is the score of the highest-scoring board. The sum/union bound would have added the 1 and the 2, resulting in an upper bound of 3. The max/no mark bound takes advantage of the fact that this cell can only be one of two possibilities, not both.
Now what if we throw a few more letters on:
| f | {a,u} | r |
| z | . | e |
| z | y | . |
With the new letters, there are more points coming from the u:
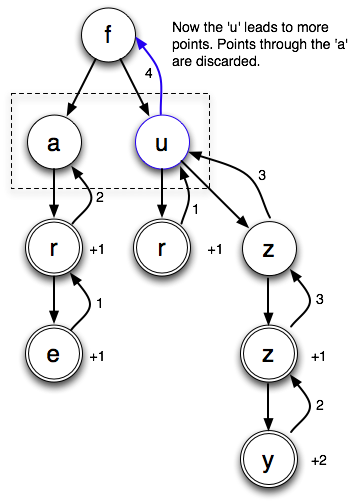
The two points going through the ‘a’ are dropped on the floor. sum/union would have resulting in a bound of 4+2. When there are lots of letter choices on every cell, you can see why max/no mark is a much tighter bound.
It’s important to note that there are two sources of branching in these search trees: (1) being able to go in multiple directions from a cell (i.e. f->u->r or z) and (2) having multiple choices on a cell (i.e. f->a or u). The max/no mark bound sums the scores resulting from choices in case (1) and takes the max of choices in case (2). The sum/union bound takes the sum in both cases.

